分子動力学シミュレーションってなに?
まずは分子動力学シミュレーションについて説明します。分子動力学シミュレーションではまず、空間(例えば100nm四方の立方体)を用意し、そこに粒子や分子を一定数(例えば1000個)配置します。その粒子や分子間にポテンシャルを与え、ニュートン力学$ma=F$に則って各粒子を動かすことで、その粒子系の静的構造や動的過程をシミュレーションする手法です。
このホームページでは下の条件(炭素Cとケイ素Siの1000粒子系)に対して分子動力学シミュレーションを行っています。
| C | Si | |
| 粒子数 | 800 | 200 |
| 質量 | 1.0 | 1.0 |

分子動力学シミュレーションで得られたキャプチャ画像が上です。青いものが炭素Cで黄色のものがケイ素Siです。
粒子間のポテンシャルはレナードジョンポテンシャル(LJポテンシャル)の形を用いています($V=4\epsilon((\sigma/r)^6-(\sigma/r)^{12})$)。$r$は粒子間の距離です。各粒子間のポテンシャルパラメータ$epsilon$と$\sigma$は下の表の通りです。
| C-C | Si-Si | C-Si、Si-C | |
| $\epsilon$ | 1.0 | 0.5 | 1.5 |
| $\sigma$ | 1.0 | 0.88 | 0.8 |
この粒子系に対し、体積と温度を次のように変化させた場合の内部エネルギー$U(T,V)$と圧力$P(T,V)$を求めました。
| 体積 | 740~800まで1刻みで変化させる |
| 温度 | 1.17~1.23まで0.001刻みで変化させる |
なお、内部エネルギー$U(T,V)$は$U(T,V)=\sum_i\frac{1}{2}m_iv_i^2+\sum_{i<j}V_{ij}$で求められ、圧力$P(T,V)$はビリアル定理から$P(T,V)=\frac{Nk_BT}{V}+\frac{1}{3V}<\sum_ir_i\cdot{F_i}>$で求めることができます。$<>$は平均値と考えてください。いずれも、分子動力学シミュレーションで得られる$v_i$や$F_i$などから計算することができます。
それでは、実際にさまざまな体積、温度で分子動力学シミュレーションを行いましたので、その結果からエントロピー$S(T,V)$を求めてみます。
MDから得られる生データ
分子動力学シミュレーションの結果から得られた内部エネルギー$U$と圧力$P$の 一部結果をまとめたものが下の表です。(圧力$P$は分子動力学シミュレーションで十分なサンプルをとることが難しく、下表で温度$T$上昇、体積$V$減少の際に圧力$P$が増加していない点が複数ありますが、ご了承願います。)
| エネルギー$U(T,V)$ | 体積$V$ | |||||||
| 800 | 790 | 780 | 770 | 760 | 750 | 740 | ||
| 温度$T$ | 1.17 | 1358 | 1391 | 1427 | 1466 | 1505 | 1557 | 1611 |
| 1.18 | 1382 | 1419 | 1444 | 1495 | 1536 | 1586 | 1634 | |
| 1.19 | 1403 | 1440 | 1473 | 1512 | 1562 | 1608 | 1658 | |
| 1.20 | 1429 | 1463 | 1497 | 1540 | 1583 | 1635 | 1687 | |
| 1.21 | 1454 | 1486 | 1526 | 1568 | 1612 | 1657 | 1711 | |
| 1.22 | 1476 | 1510 | 1550 | 1591 | 1633 | 1680 | 1737 | |
| 1.23 | 1500 | 1531 | 1576 | 1617 | 1656 | 1706 | 1764 | |
| 圧力$P(T,V)$ | 体積$V$ | |||||||
| 800 | 790 | 780 | 770 | 760 | 750 | 740 | ||
| 温度$T$ | 1.17 | 1.445 | 1.491 | 1.486 | 1.488 | 1.569 | 1.536 | 1.564 |
| 1.18 | 1.484 | 1.504 | 1.520 | 1.513 | 1.552 | 1.605 | 1.515 | |
| 1.19 | 1.441 | 1.513 | 1.501 | 1.564 | 1.565 | 1.559 | 1.618 | |
| 1.20 | 1.527 | 1.524 | 1.559 | 1.554 | 1.577 | 1.565 | 1.606 | |
| 1.21 | 1.512 | 1.546 | 1.512 | 1.561 | 1.576 | 1.636 | 1.65 | |
| 1.22 | 1.515 | 1.564 | 1.593 | 1.580 | 1.620 | 1.631 | 1.663 | |
| 1.23 | 1.515 | 1.517 | 1.574 | 1.618 | 1.613 | 1.667 | 1.641 | |
$U(T,V)$が自然でないことを確認
ここからがこのページの本題です。まずは分子動力学シミュレーションの結果から$U=U(T,V)$が自然な変数の組になっていないことを確認しましょう。
分子動力学シミュレーションの結果から、様々な$T,V$におけるエネルギーが分かっています。これは$U=U(T,V)$が分かっているということを意味しています。
ただ、$U$の自然な変数は$U(S,V)$であると言われています。現に、いま得られている$U(T,V)$を温度$T$で微分した値$(2542.12542.1)$は熱力学的によくわからない値になっています(圧力$P$や体積$V$等の数値になっていない)。
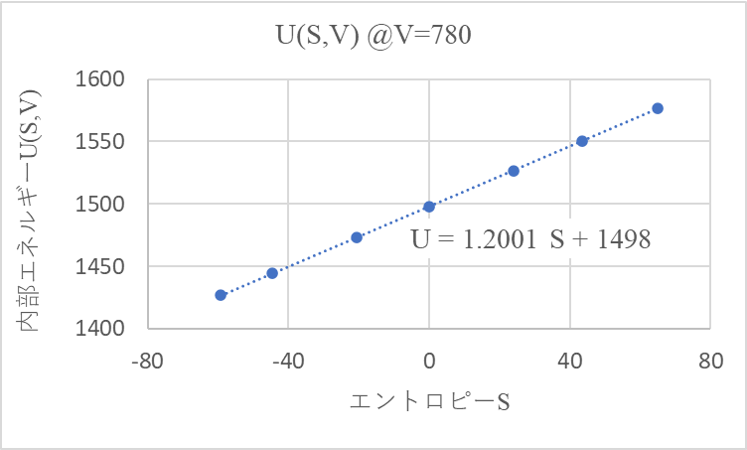
つまり、$U(T,V)$は自然な変数になっていません。
MDの結果からエントロピー$S$を計算する
それではいよいよ、分子動力学シミュレーションから得られた結果から、エントロピー$S$を求めます。
熱力学第一法則$ΔU=TΔS−PΔV$を利用すると、エントロピー$S$の変化量は$ΔS=\frac{1}{T}ΔU+\frac{P}{T}$で得られます。この式にMDから得られている$U,T,P$を一つずつ代入し、$\Delta{S}$を求めます。
注意点として、エントロピーは$ΔS$の変化量しか計算できないため、どこかを熱力学的状態を基準として、他の熱力学状態でのエントロピーを計算する必要があります。そこで本ホームぺージでは$T=1.20,V=780$の時の$S$を$0$とします。
$\Delta{T}$変化時の$\Delta{S}$計算
それではまず、試しに$T=1.200→1.201$へ系が$V=780$を保ったまま等積昇温した時のエントロピー変化を考えましょう。分子動力学シミュレーションの結果から得られている$U$の 値は以下です。
| 温度$T$ | 1.200 | → | 1.201 |
| 体積$V$ | 780 | → | → |
| 内部エネルギー$U$ | 1497.6 | → | 1504.6 |
| エントロピー$S$ | 0 | → | ? |
この変化では、$ΔV=0$であることから、エントロピー変化$ΔS$は$ΔS=\frac{1}{T}ΔU+\frac{P}{T}ΔV=\frac{1}{T}ΔU$で計算できます。$ΔU=1504.6−1497.6=7.0$であるため、$ΔS=\frac{1}{T}ΔU=1/1.20×7.0=5.83$で、$S(T=1.2,V=780)$を$0$としていることから、$S(T=1.201,V=780)=5.83$となります。
| 温度$T$ | 1.200 | → | 1.201 |
| 体積$V$ | 780 | → | → |
| エントロピー$S$ | 0 | → | 5.83 |
$\Delta{V}$変化時の$\Delta{S}$計算
次に、$V=780→781$へ系が$T=1.2$を保ったまま定温膨張した時のエントロピー変化を考えましょう。分子動力学シミュレーションの結果から得られている$U$の値は以下です。この時の$\Delta{S}$を求めましょう。
| 体積$T$ | 780 | → | 781 |
| 温度$T$ | 1.20 | → | → |
| 圧力$P$ | 1.559 | → | 1.559 |
| 内部エネルギー$U$ | 1497.6 | → | 1497.0 |
| エントロピー$S$ | 0 | → | ? |
エントロピー変化$ΔS$は $ΔS=\frac{1}{T}ΔU+\frac{P}{T}ΔV$で計算できます。$ΔU=1497.0−1497.6=−0.6$と$ΔV=781−780=1$であることと、圧力の平均値$P=1.559$を用いると$ΔS=\frac{1}{T}ΔU+\frac{P}{T}ΔV=0.799$とエントロピー変化を計算することができます。
| 体積$V$ | 780 | → | 781 |
| 温度$T$ | 1.20 | → | → |
| エントロピー$S$ | 0 | → | 0.799 |
エントロピー$S(T,V)$まとめ
上の例では、$S(T=1.201,V=780)$と$S(T=1.20,V=781)$を計算できていることになります。
このように$ΔV$と$ΔT$の変化ごとの$ΔU,ΔV$を利用することで基準からの エントロピー変化量$ΔS$を計算することができます。
さらにどんどん計算を行い、$T:1.18~1.22$と$V:740~800$の領域でエントロピー変化を計算すると下記のようになります。(計算自体はEXCELなどでまとめてできるため、手間は多くありません。)
| エントロピー$S(T,V)$ | 体積$V$ | |||||||
| 800 | 790 | 780 | 770 | 760 | 750 | 740 | ||
| 温度$T$ | 1.17 | −91.3 | −76.7 | −59.2 | −39.5 | −20.2 | 9.8 | 41.7 |
| 1.18 | −71.1 | −52.8 | −44.5 | −14.8 | 6.0 | 34.2 | 61.0 | |
| 1.19 | −53.5 | −35.0 | −20.5 | −1.0 | 28.1 | 53.0 | 81.6 | |
| 1.20 | −31.8 | −15.6 | 0.0 | 22.9 | 45.5 | 75.2 | 105 | |
| 1.21 | −10.3 | 3.0 | 24.0 | 46.2 | 69.2 | 94.0 | 125 | |
| 1.22 | 7.5 | 23.0 | 43.5 | 64.5 | 86.9 | 113 | 147 | |
| 1.23 | 27.1 | 40.2 | 64.9 | 85.7 | 105 | 134 | 168 | |
以上の計算からエントロピー$S$(特に$S(T,V)$)を得ることができます。
次のページではこの$S(T,V)$を利用して$U(T,V)$を$U(S,V)$へ書き換え、$U$に対しては$S,V$が自然な変数となっていることを確認します。



